Monte Carlo Methods

Statistical Inference

R Packages

library(tidyverse)
library(palmerpenguins)

theme_set(theme_bw())
theme_update(axis.title = element_text(size = 24))


tuesdata <- tidytuesdayR::tt_load(2020, week = 28)
#> 
#>  Downloading file 1 of 1: `coffee_ratings.csv`
coffee_ratings <- tuesdata$coffee_ratings
coffee_aroma <- coffee_ratings |> filter(aroma > 5.5)

shuffle <- function(x){
  n <- length(x)
  return(sample(x, n))
}

penguins <- penguins |> drop_na()

Power Analysis

  • Power Analysis

  • Resampling Techniques

  • Permutation Tests

Type 1 and 2 Error

Code 
a1 <- data.frame(
   x = c(2.5,3.5),
   y = c(41, 41),
   label = c("Yes", "No")
)

a2 <- data.frame(
   x = c(1.9),
   y = c(25, 35),
   label = c("False", "True")
)
a3 <- tibble(x = c(1.7,3), 
             y = c(30, 43), 
             label = c("H0", "Reject H0"))

yay <- tibble(x = c(2.5, 3.5), 
              y = c(25, 35), 
              label = c("Yay!", "Yay!"))

type1 <- tibble(x = c(2.5, 3.5),
                y = c(36.5, 26.5),
                label = c("Type I Error", "Type II Error"))

type2 <- tibble(x = c(3.5, 2.5),
                y = c(24.5, 34.5),
                label = c("beta", "alpha"))


# basic graph
p <- ggplot() + theme_void()

# Add rectangles
p + annotate("rect", 
             xmin=c(2,3), xmax=c(3,4), 
             ymin=c(20,20), ymax=c(30,30), 
             alpha=0.2, color="green", fill="green") + 
    annotate("rect", 
             xmin=c(2,3), xmax=c(3,4), 
             ymin=c(30,30), ymax=c(40,40), 
             alpha=0.2, color="red", fill="red") +
    annotate("rect",
             xmin=c(3,2), xmax=c(4,3),
             ymin=c(30, 20), ymax=c(40, 30),
             alpha=0.8, color="royalblue", fill="royalblue") +
    geom_text(data=a1, aes(x=x, y=y, label=label),
             size=10 , fontface="bold" ) +
    geom_text(data=a3, aes(x=x, y=y, label=label),
             size=10 , fontface="bold.italic" ) +
    geom_text(data=a2, aes(x=x, y=y, label=label),
             size=10, angle = 90, fontface="bold" ) +
    geom_text(data=yay, aes(x=x, y=y, label=label),
             size=10, fontface="bold.italic" ) +
    geom_text(data=type1, aes(x=x, y=y, label=label),
             size=10, fontface="bold") +
    geom_text(data=type2, aes(x=x, y=y, label=label),
             size=10, fontface="bold", parse = T )

Type 1 and 2 Error

Code 
x <- seq(-4, 4, length.out = 1000)
xx <- seq(-1, 7, length.out = 1000)
dt_one<-function(x){
            y <- dnorm(x)
            y[x < qnorm(.94)] <-NA
            return(y)
}
dt_two<-function(x){
            y <- dnorm(x, mean = 3)
            y[x > 1.645] <-NA
            return(y)
}
df1 <- tibble(x = x, y = dnorm(x))
df2 <- tibble(x = xx, y = dnorm(xx, mean = 3))

a1 <- tibble(x = c(0,3), y = c(0.43, 0.43), label = c("H0", "H1"))
a2 <- tibble(x = c(2.05,1.25), y = c(0.02, 0.02), label = c(paste("alpha"), "beta"))

df1 |> 
  ggplot(aes(x, y)) +
    stat_function(fun = dt_one, geom = "area", fill = "red") +
    geom_line() +
    geom_line(aes(x, y), df2) +
    stat_function(fun = dt_two, geom = "area", fill = "green") +
    geom_vline(aes(xintercept = 1.645), lwd = 1.5) +
    geom_text(data=a1, aes(x=x,y=y, label=label),
              size=14 , fontface="bold.italic" ) +
    geom_text(data=a2, aes(x=x,y=y, label=label),
              size=10 , fontface="bold.italic", parse = T) +
    theme_bw()

Power

Power is the probability of rejecting \(H_0\) given that \(H_1\).

\[ Power = 1-\beta \]

Power

We want to ensure we have a high power and low type I error rate (\(\alpha\)).

As practitioners, we control \(\alpha\). Set it before we conduct a study. Usually set at 0.05.

We cannot control power because it is dependent by effect size, \(\alpha\), and sample size.

Power Relationships

  • \(\alpha \uparrow\) \(\rightarrow\) \(Power\ \uparrow\)
  • \(n \uparrow\) \(\rightarrow\) \(Power\ \uparrow\)

Power Analysis in R

The pwr package in R will conduct power and sample size for several common statistical tests. For more information, you can check this vignette and their github.

Conceptial

Code 
x <- seq(-4, 4, length.out = 1000)
xx <- seq(-1, 7, length.out = 1000)
dt_one<-function(x){
            y <- dnorm(x)
            y[x < qnorm(.94)] <-NA
            return(y)
}
dt_two<-function(x){
            y <- dnorm(x, mean = 3)
            y[x > 1.645] <-NA
            return(y)
}
df1 <- tibble(x = x, y = dnorm(x))
df2 <- tibble(x = xx, y = dnorm(xx, mean = 3))

a1 <- tibble(x = c(0,3), y = c(0.43, 0.43), label = c("H0", "H1"))
a2 <- tibble(x = c(2.05,1.25), y = c(0.02, 0.02), label = c(paste("alpha"), "beta"))

df1 |> 
  ggplot(aes(x, y)) +
    stat_function(fun = dt_one, geom = "area", fill = "red") +
    geom_line() +
    geom_line(aes(x, y), df2) +
    stat_function(fun = dt_two, geom = "area", fill = "green") +
    geom_vline(aes(xintercept = 1.645), lwd = 1.5) +
    geom_text(data=a1, aes(x=x,y=y, label=label),
              size=14 , fontface="bold.italic" ) +
    geom_text(data=a2, aes(x=x,y=y, label=label),
              size=10 , fontface="bold.italic", parse = T) +
    theme_bw()

Monte Carlo Power Analysis

Given a Null and Alternative hypothesis, one can determine how often a you will reject the null hypothesis from a high number of simulated data.

This is done by simulating from a hypothesized alternative distribution, conducting a hypothesis test given that the null hypothesis is true, and determine how often do you reject the null hypothesis.

\[ Power = \frac{\#\ Rejected}{\#\ Simulated\ Data} \]

Monte Carlo Power Analysis

  1. Construct an alternative hypothesized distribution (\(\mu = \mu_a\))
  2. Simulate from the alternative hypothesized distribution
  3. Compute the test statistic based on null hypothesis distribution
  4. Determine and record if the test statistic is rejected or not
  5. Repeat steps 2-4 \(N\) times
  6. Find the proportion rejected from the simulation study

t-test Example

Use a Monte Carlo Hypothesis Test for \(H_0: \mu = 6\) and \(H_a: \mu \neq 6\). Simulate fake data from 24 RV’s from \(N(3, 9)\). Testing how the distribution will look like assuming that the null hypothesis is true.

Code 
x <- rnorm(24, 3, 3)

Answer:

Code 
tstat <- (mean(x) - 6)/(sd(x)/sqrt(24))


t_stat_sim <- function(i){
  x <- rnorm(24, 6, 3)
  tt <- (mean(x) - 6)/(sd(x)/sqrt(24))
  return(tt)
}
t_dist <- sapply(1:100000, t_stat_sim)

t_dist |> tibble(x = _) |> 
  ggplot(aes(x, y = ..density..)) +
  geom_histogram() +
  geom_vline(aes(xintercept = tstat), col = "red")

sum(abs(tstat) < abs(t_dist))
(sum(abs(tstat) < abs(t_dist)) + 1) / (length(t_dist) + 1)

Power Analysis Example

Code 
alpha <- 0.05
cv <- qt(1-alpha/2, 23)

t_stat_sim <- function(i, mu){
  x <- rnorm(24, mu, 3)
  tt <- (mean(x) - 6)/(sd(x)/sqrt(24))
  return(cv < abs(tt))
}
mus <- 0:12
powers <- c()
for(i in 1:13){
  t_dist <- sapply(1:100000, t_stat_sim, mu = mus[i])
  powers <- c(powers, mean(t_dist))
}

tibble(x = mus, y = powers) |> 
  ggplot(aes(x, y)) +
  geom_line() +
  ylab("Power") +
  xlab("Alternative")

Resampling Techniques

  • Power Analysis

  • Resampling Techniques

  • Permutation Tests

Resampling Techniques

Resampling techniques involve methods that require to sample from the data, instead of the parametric model. Common Methods:

  • Permutation Tests
  • Boostrapping
  • Cross-Validation
  • Jackknifer

Sampling with Replacement

Given a data set, we sample an observation to a new data set. The sampled observation can be resampled again to the new data set.

Code 
x <- 1:20
sample(x, 10, replace = T)
#>  [1] 11 16  3 18  8  1  9 10 16 14

Sampling without Replacement

Given a data set, we sample an observation to a new data set. The sampled observation cannot be resampled again to the new data set.

Code 
x <- 1:20
sample(x, 10, replace = F)
#>  [1] 12  8  1  4  6  3 11 13 14 15

Permutation Tests

  • Power Analysis

  • Resampling Techniques

  • Permutation Tests

Permutation Tests

Permutation tests conducts a statistical test by constructing the null distribution by rearranging the data points in a sample.

Null hypothesis states that the rearrangements of the data points are random.

Alternative hypothesis states that the rearrangement of the data points aren’t random.

Permutation Distributions

Null

\[ F_x = F_y \]

Alternative

\[ F_x \neq F_y \]

Permutation Distributions

Suppose \(\{X_i, Y_i\}^n_{i=1}\) is an observed permutation, \(X = \{X_1, \ldots, X_n\}\), \(Y = \{Y_1, \ldots, Y_n\}\).

The Probability of any permuation is \(1/n!\).

Therefore, for a statistic \(T(X,Y)\), a sampling distribution can be constructed by all the different permutations.

A hypothesis test can be conducted by observing the proportion of more extreme values of the sample statistic.

Approximate Permutation Distribution

Constructing the distribution for the permutations can be challenging if the number of permutations is high! If \(n=100\), the number of permutations is \(100!\):

factorial(100)
#> [1] 9.332622e+157

Therefore, simulation techniques are needed to approximate the p-value.

By randomly drawing from the sample, we can approximate the p-value.

Algorithm

  1. Construct a new data set
  2. Fix the predictor (\(X\)) variable and randomly assign a data point \(Y\) to the fixed \(X\)
  3. Compute a test statistic using the new data set and store the value
  4. Repeat steps 1 and 2 for \(N\) times
  5. Compute the test statistic from the empirical sample (un-permutated)
  6. Count how many permutated statistics that are more extreme than the sample test statistic (\(m\))
  7. Compute the Monte Carlo p-value

\[ p = \frac{m +1}{N + 1} \]

Example: Emperical Data

Code 
penguins |> ggplot(aes(x=species, y = body_mass_g)) +
  geom_boxplot() +
  geom_jitter() +
  labs(x = "Species", y = "Body Mass")

Example: Random Shuffling

Code 
penguins |> ggplot() +
  labs(x = "Species", y = "Body Mass") + 
  geom_jitter(aes(species, shuffle(body_mass_g)))

Example: Random/Emperical

Code 
penguins |> ggplot(aes(x = species, y = body_mass_g)) +
  labs(x = "Species", y = "Body Mass") + 
  geom_jitter(col = "red") +
  geom_jitter(aes(species, shuffle(body_mass_g)))

Example: Random/Emperical

Code 
penguins |> ggplot(aes(x = species, y = body_mass_g)) +
  labs(x = "Species", y = "Body Mass") + 
  geom_jitter(aes(species, shuffle(body_mass_g))) +
  geom_jitter(aes(species, shuffle(body_mass_g))) +
  geom_jitter(aes(species, shuffle(body_mass_g))) +
  geom_jitter(aes(species, shuffle(body_mass_g))) +
  geom_jitter(aes(species, shuffle(body_mass_g))) +
  geom_jitter(aes(species, shuffle(body_mass_g))) +
  geom_jitter(aes(species, shuffle(body_mass_g))) +
  geom_jitter(aes(species, shuffle(body_mass_g))) +
  geom_jitter(aes(species, shuffle(body_mass_g))) +
  geom_jitter(aes(species, shuffle(body_mass_g))) +
  geom_jitter(col = "red")

ANOVA

We want to determine if body mass of penguins are different for different species.

Code 
penguins |> aov(body_mass_g ~ species, data = _) |> anova()
#> Analysis of Variance Table
#> 
#> Response: body_mass_g
#>            Df    Sum Sq  Mean Sq F value    Pr(>F)    
#> species     2 145190219 72595110  341.89 < 2.2e-16 ***
#> Residuals 330  70069447   212332                      
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Permutation Test

Code 
f_stat <- penguins |> 
  aov(body_mass_g ~ species, data = _) |> 
  anova() |> 
  _$`F value`[1]
  

f_sim <- function(i){
  ff <- penguins |> 
    aov(shuffle(body_mass_g) ~ species, data = _) |> 
    anova() |> 
    _$`F value`[1]
  return(ff)
}

f_dist <- replicate(10000, f_sim(1))

tibble(x= f_dist) |> 
  ggplot(aes(x, y = ..density..)) +
  geom_histogram() +
  geom_vline(xintercept = f_stat)
Code 
sum(f_stat < f_dist) + 1 / (length(f_dist) + 1)
#> [1] 9.999e-05

Permutation Example

Is there a linear relationship between flavor and aroma in coffee drinks from the coffee_aroma data set.

Code 
coffee_aroma |> ggplot(aes(x=aroma, y = flavor)) +
  geom_point() + theme_bw() +
  geom_smooth(method = "lm", se = F)

Permutation Linear Regression

  • Keep the predictor values fixed (unchanged)
  • Randomly assign the sampled outcome values to a fixed predictor
  • Compute the regression coefficients for the predictor variable

Simulated Permutation

Code 
coffee_aroma |> ggplot(aes(x=aroma, y = shuffle(flavor))) +
  geom_point() + theme_bw() +
  geom_smooth(method = "lm", se = F)

Permutations

Code 
coffee_aroma |> ggplot() +
  geom_smooth(mapping = aes(aroma, flavor), method = "lm", se = F, col = "red") +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F) +
  geom_smooth(mapping = aes(aroma, shuffle(flavor)), method = "lm", se = F)

Permutation Test

Code 
f_stat <- coffee_aroma |> 
  lm(flavor ~ aroma, data = _) |> 
  _$`coefficients`[2]



f_sim <- function(i){
  ff <- coffee_aroma |> 
  lm(shuffle(flavor) ~ aroma, data = _) |> 
  _$`coefficients`[2]
  return(ff)
}

f_dist <- replicate(10000, f_sim(1))

tibble(x= f_dist) |> 
  ggplot(aes(x, y = ..density..)) +
  geom_histogram() +
  geom_vline(xintercept = f_stat)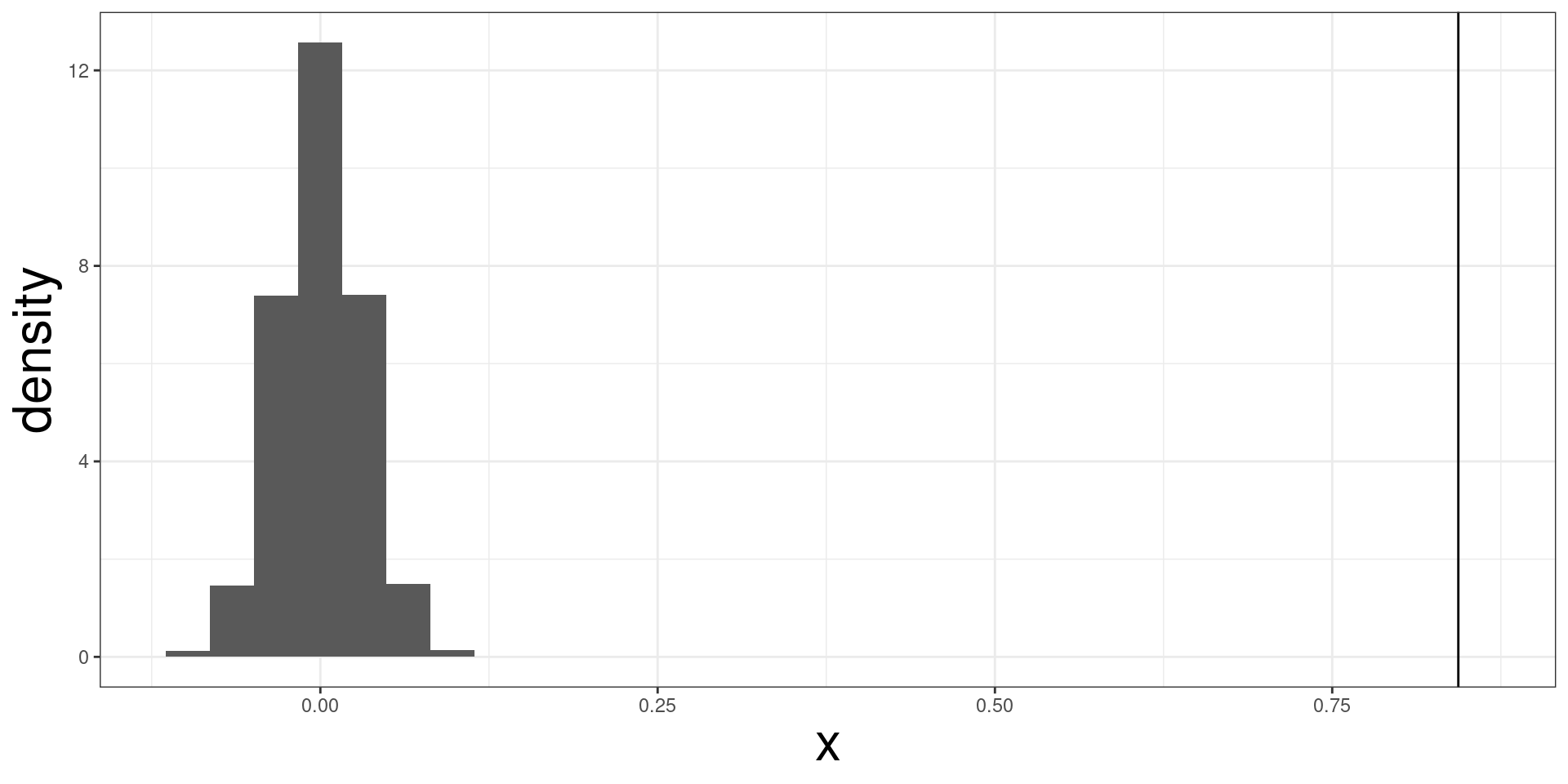

Code 
sum(f_stat < f_dist) + 1 / (length(f_dist) + 1)
#> [1] 9.999e-05